Engine Thermodynamics

The study of engines is really the study of thermodynamics, the study of the movement of heat. The four-stroke engine in the M5 is an example of a heat engine. The explosion of the fuel releases heat as part of a chemical reaction, and that heat energy is converted into a different kind of energy: work - the application of a force over a distance that moves the car.

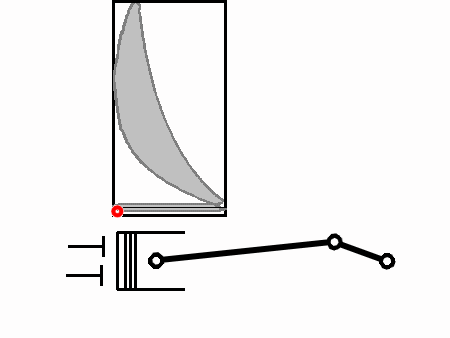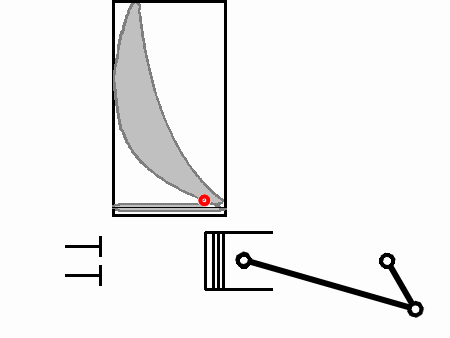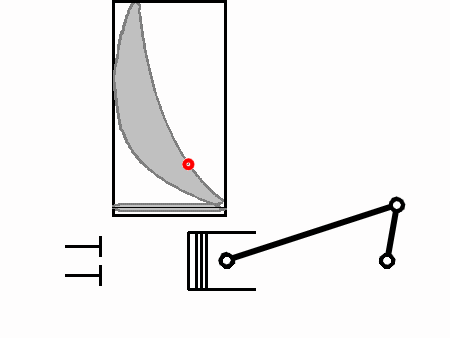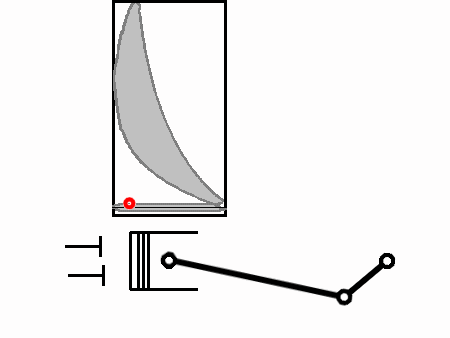
A very useful tool in understanding how a heat engine functions is the p-V diagram. This diagram plots pressure versus volume inside the cylinder. The pressure in question is the pressure above the piston, the volume in question is the volume above the piston.

Area in the p-V diagram corresponds to energy (work). Pressure is a kind of potential energy. If the result of a pressure is to move a piston so as to change the volume by dV (in cubic inches) and the pressure by dp (in pounds per square inches), the product dp*dV has units of pound-inches, or force over a distance, which is work energy.

Bearing in mind that work corresponds to area in the p-V diagram, the following p-V diagram is for an idealized four-stroke (Otto cycle) engine. "Idealized" means

• a completely free-flowing intake and exhaust,
• instantaneous combustion of all the fuel,
• instantaneous opening and closing of valves,
• no momentum to the gasses,
• no gain or loss of heat (called an adiabtic process in thermodynamics).

Along the vertical axis is the gas pressure inside the cylinder (p). Along the horizontal axis is the volume of the cylinder above the piston, varied as the piston moves back and forth (V). The four-stroke Otto cycle follows the path 1-2-3-4-5-6-1-2-3-... and so on, as shown below.

Assuming completely free-flowing intake and exhaust, the pressure in the cylinder is at atmospheric pressure during both the intake stroke (1→2) and the exhaust stroke (6→1). During the intake stroke the volume of the cylinder increases because the piston moves. During the compression stroke (2→3), the valves are closed and the pressure rises as the gas is squeezed into a smaller volume. We'll explain the curved shape between 2 and 3 (and 4 and 5) in a moment.

At 3 the spark is ignited, the fuel is instantly combusted, and heat is released. The released heat instantaneously increases the pressure in the cylinder according to the Ideal Gas Law

pV = nRT

This law says that for any gas, air included (we can ignore the fuel mixed in for now), pressure (p) times volume (V) for a given quantity of air molecules (n) are both directly proportionate to temperature (expressed in degrees Kelvin: Celsius degrees above absolute zero which is -273.15 Celsius). R is a constant of proportionality called Avogadro's constant.

So when T instantly rises as a result of the explosion  the piston has had no time to move, hence V is unchanged, the amount of air in there (n) is also unchanged, so it is pressure (p) that must rise instantaneously. Hence the rise from 3 to 4.

From 4 to 5 is the power stroke during which  work is done to the piston head (Force over a distance). During this time the volume increases as the piston moves down and the pressure also decreases.

Between 5 and 6 the exhaust valves are instantaneously opened and the pressure immediately equalizes to atmospheric pressure (due to the completely free-flowing exhaust). Because of the pressure drop, heat is also lost to the flow of exhaust (but not as much heat is lost as was gained previously, the rest having been converted to work).

Finally the exhaust is pushed out through the exhaust stroke from 6 to 1, and the cycle repeats.

The reason for the curved shape between 2-3 and 4-5 is as follows.

One might naively assume by looking at the Ideal Gas Law above that p and V should vary in a proportionate way. That is, if V goes down by a factor of 10 (as it does in the M5), then p should go up by a factor of 10. But while we see volume going down by a lot, pressure does not rise as much as this. This is because temperate is not constant as air is squeezed. In fact, assuming no heat is gained or lost through the piston walls, then

T = C * p^(2/f+2)

The quantity f is the number of degrees of movement freedom of the gas molecules. Air is mainly made up of N2 and O2, which are both two-atom molecules. They have 5 degrees of freedom (the pair of atoms can move around in 3 dimensions, and the two atoms can move in 2 additional dimensions relative to one another and still not break, making f = 5 for air). Thus temperature (in Kelvin) rises in proportion to the 7th root of pressure squared.

We can then plug this into the Ideal Gas Law to get that

p = C / V^(7/5)

This relation between pressure and volume gives us the curved shape between 2-3 and 4-5.

The crucial part is that from 2 to 3 work is done by the piston, and from 4 to 5, work is done to the piston. The net work applied to the crankshaft in one complete cycle is proportional to the area outlined by 3,4,5,6.

This is the theory of the Otto engine. In practice, none of the idealized assumptions are valid, and so a more realistic p-V diagram for an Otto cycle is shown below.

The more important deviations from ideal are as follows.

1. During the compression stroke heat is being generated and is being lost through the cylinder walls to the cooling system. 
2. Towards the end of the compression stroke the spark is fired, because in reality combustion takes time and before it is finished the piston has already hit Top-Dead-Center and is returning while the pressure continues to rise due to the combustion.
3. During the power stroke more heat is lost to the surroundings, and hence the shape is not the idealized adiabatic one.
4. Because the valves do not move instantaneously, the exhaust valve must start opening while the piston is still moving down as it must be mostly open before the exhaust stroke happens or even more work will be required to move the piston back.
5. All of the above change the shape of the work loop, making it smaller than in the ideal situation.
6. During the exhaust stroke the air is backed up by the exhaust system and the piston must work against that backup. Hence we see the pressure in the cylinder is higher that atmospheric.
7. On the intake stroke there is always a partial vacuum in the intake manifold, and hence work must be done against that vacuum.
8. At cylinder Bottom-Dead-Centre the closing of the intake valve takes some time.
9. The area enclosed by the lower loop is net negative work called "pumping losses". This offsets the positive work done in the upper loop with the net work being the difference between the two.

Actual pumping losses from a multi-cylinder engine are shown below, with each line representing a different cylinder. As you can see, the situation is actually much more complicated than the simple illustrations show!

Pumping losses are the main controllable factor in an engine design. The pumping losses are high both at low engine speed when the incoming air is restricted, thus affecting fuel economy; and at high engine speed when the air cannot go in or be pushed out fast enough, thus affecting both fuel economy and performance.

At high engine speed, pumping losses can be reduced by "de-throttling" the air going into the cylinders allowing the engine to "breathe" more freely. This is done at the air intake, air filter, throttle, intake manifold, and intake valves.

High engine speed pumping losses can also be minimized by freeing up the outgoing flow of exhaust gasses through the exhaust manifold, catalytic converter, muffler, and exhaust pipes.

This freeing up of the airflow helps keep the air pressure the same during intake and exhaust strokes, thus minimizing the area within the pumping loss loop and maximizing the area of the power loop.

On the intake stroke we are drawing air in at "Intake Manifold Pressure", which is lower than atmospheric pressure. This is because we cannot feed air in fast enough in general for the cylinders and a partial vacuum is created in the intake manifold. On the exhaust stroke, the pressure is slightly above atmospheric pressure, as we are trying to push the exhaust gasses out through the exhaust system which gets "backed up" a little due to the relatively narrow valves, pipes, catalytic converts, mufflers, and tail pipes.

In the normal Otto cycle, the area surrounded by 5,6,7 below is wasted work that is blown out the exhaust valves (heated and pressurized gasses). 

In other words, had the piston stroke been longer, we could have used that work, but as it is, we had to dump it all out the exhaust. It is possible to recoup some of that work and put it to good use. This is the job of the turbochargers. The M5 has turbos that are spun using some of the otherwise wasted energy in the exhaust gasses. The turbines then spin compressors, which are used to compress the air going into the cylinders. The compressed air has more Oxygen and can therefore support a larger explosion.

As it relates to the p-V diagram, the effect of the turbo is to raise the intake manifold pressure well above atmospheric. However, that comes at the expense of also having to raise the exhaust manifold pressure, as there is a pushback from the turbos. The net of all of this is that everything in the p-V diagram is just raised upwards, with just a bit of net loss coming from the less than 100% efficiency of the turbocharger. In other words, even though the piston has to work harder at pushing exhaust out and this robs power, the pre-compressed air entering the cylinder adds back almost the same amount of work to the piston.

However, any small net losses here are more than made up for by the fact that the pressurized air can support a larger quantity of fuel, and hence the rise between 3 and 4 can be much greater as a result with a dramatic increase in net positive work overall.