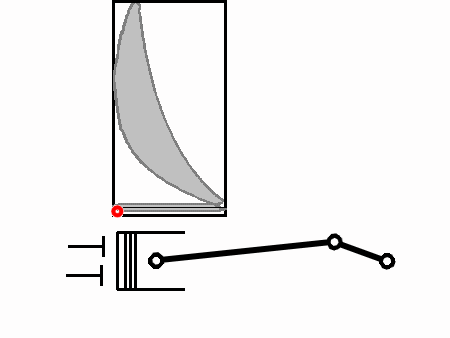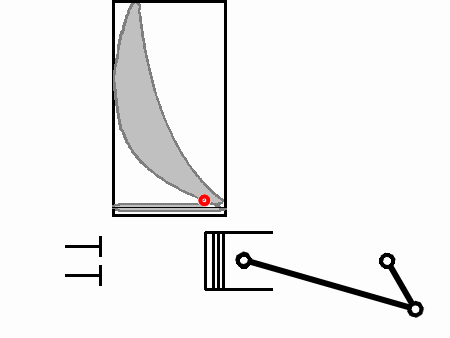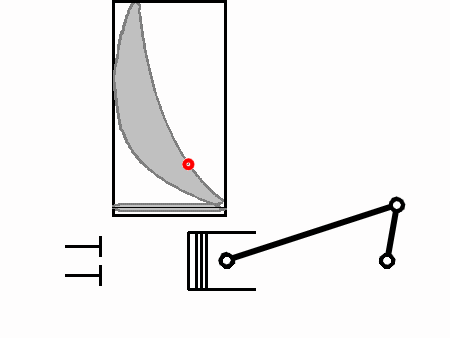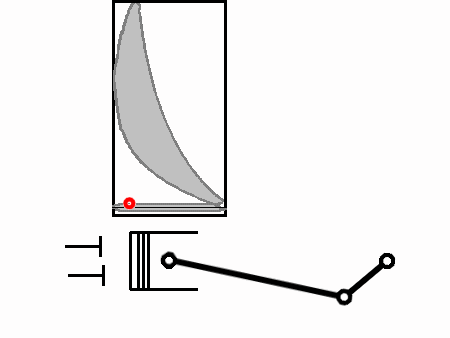
There are two main types of FI engines. One is called "Supercharged", where the air compressor is run by fan belts driven by the crankshaft.
A key design issue with turbos is minimizing "turbo lag", the time between when you apply your foot to the gas and when full torque is available. My old turbocharged Volvo S70 T5 had lag. You would push the accelerator and get regular non-turbocharged acceleration, and then about a second later the acceleration would kick up a notch, this time turbo-powered! While a delightful surprise, it did mean you were bit slow off the mark when trying to accelerate hard.
Most of BMW and M's intellectual energy went into solving this issue which is not at all present in naturally aspirated engines and the reason BMW stayed away from turbos for so long. They did a lot of work on this for the N63 engine in the 550i, more still for the S63 in X5 M, and even more still for the S63top in the M5. in fact, most of the development effort in the S63top was to decrease turbo lag over the S63, not particularly to add horsepower. The proof is in the pudding, and there is no noticeable turbo lag on the car.
One reason for lag is because the exhaust gasses have a ways to flow before hitting the turbo. Normally, V engines intake in the middle of the V and exhaust towards the outside of the V. In the M5 motor, these are switched so as to minimize the distance from exhaust ports to turbos that can therefore be nestled on the inside of the V. These exceptionally short paths are shown clearly in the above illustration.
The following illustration shows the intake airflow.
To help further reduce turbo lag, when in "Sport" engine mode the wastegate is kept closed longer. This leads to increased fuel consumption as the exhaust is backed up, but increases response as the turbos are kept better spooled up in case they are needed.
One consequence of the compression of the air is that it heats up to over 130 C. To allow more fuel to be mixed in and keep the compression ratio in the cylinders up, the charge air is cooled by two very large water-cooled charge air coolers back to around 50 C. These are especially large to promote better cooling, to de-throttle the intake air, and to reduce the distance to promote faster throttle response. The charge air coolers are the two prominent metal boxes at the front of the engine.
The problem with the V8 burble is that the exhaust pulses on each cylinder bank are irregular. This tends to throttle the exhaust flow. In the case of a turbocharger, the irregular pulses lead to a pulsating acceleration and deceleration of the exhaust turbines which is inefficient. To counteract this problem, BMW designed an ingenious (and patented) "crossbank exhaust manifold".
On the exhaust stroke the exhaust valves open and the returning piston drives the hot exhaust gasses out into the exhaust manifold where they are crossed over and enter into the turbos (6). A wastegate valve (7) operated by an electro-pneumatic pressure converter (8) is used to slow down the turbines when necessary. The exhaust gasses then flow out to the exhaust through the catalytic converters (11), which includes a control oxygen sensor (9) and a monitoring oxygen sensor (10).
Superchargers are often found in American muscle cars such as the 640 HP 2013 Corvette ZR1.
The other is called "Turbocharged". This engine type uses exhaust gasses to spin a turbine which in turns spins a compressor that compresses the fresh air headed for the cylinders.
This is what is used in the F10 M5 and is the essential difference between the NA engine in my old E60 545i making 325 HP, and the FI engine F10 M5 making 560 HP. The engines are very similar otherwise: both 8 cylinders, 4.4L of displacement, 4 valves per cylinder, 10:1 compression ratio, fuel injection, variable valve timing and lift. All the other major differences are to keep up with the increased output (better cooling, better lubrication, higher-strength components, and so on).
There are in fact two turbos in the F10 M5, each feeding its own cylinder bank, but getting exhaust from cylinders on both banks. Each turbo is of the twin-scroll design, meaning the exhaust is fed into two separate streams hitting different parts of the turbine wheel. The main advantage is that the two separate streams do not interfere with one another as much. In particular, you don't want an exhaust pulse from cylinder A to partially hit the turbine, and partially run back up a pipe to cylinder B's exhaust thereby putting unneeded back pressure on the exhaust.
The image below is a cut away of a turbo that shows the important components.
The exhaust side is on the left, and we see it is of the twin scroll design because of the two separate inlet channels and the corresponding shape of the turbine veins. Exhaust exits through the centre. The compressor side is on the right. Air is drawn in from the centre, compressed by the wheel, and pushed out through the single channel. In the middle is the bearing assembly. Oil is fed in from the top, directed to the ball bearings, and flows out through the bottom.
The spinning materials are all very strong and lightweight to allow it to spin up fast and without a lot of internal resistance. Turbos can spin at up to 200,000 RPM. The turbos are manufactured by Honewell Turbo Technologies, formerly Garrett who were pioneers in turbo technologies from California and who powered the very first production turbocharged car, the Oldsmobile Jetfire Rocket from the early 60's.
In the M5, the maximum boost pressure above atmospheric pressure (called "gauge pressure") is 1.5 bars (1 bar is about 1 atmosphere = 14 pounds per square inch - psi). Therefore the air is compressed to 21 psi gauge, or 35 psi absolute at sea level. The actual amount of boost changes as the exhaust flows change and as the so-called wastegate valve is manipulated by the DME (Digital Motor Electronics computer). The wastegate allows exhaust to bypass the turbine wheels in order to control boost pressure.
The M5 turbos are shown in the image below. The exhaust end is facing us, and the exhaust manifold is shown feeding the exhaust to the turbines. The compressors are on the far side, taking air in from the larger pipes in the centre, and directing it out through the smaller ones on top.
A key design issue with turbos is minimizing "turbo lag", the time between when you apply your foot to the gas and when full torque is available. My old turbocharged Volvo S70 T5 had lag. You would push the accelerator and get regular non-turbocharged acceleration, and then about a second later the acceleration would kick up a notch, this time turbo-powered! While a delightful surprise, it did mean you were bit slow off the mark when trying to accelerate hard.
Most of BMW and M's intellectual energy went into solving this issue which is not at all present in naturally aspirated engines and the reason BMW stayed away from turbos for so long. They did a lot of work on this for the N63 engine in the 550i, more still for the S63 in X5 M, and even more still for the S63top in the M5. in fact, most of the development effort in the S63top was to decrease turbo lag over the S63, not particularly to add horsepower. The proof is in the pudding, and there is no noticeable turbo lag on the car.
One reason for lag is because the exhaust gasses have a ways to flow before hitting the turbo. Normally, V engines intake in the middle of the V and exhaust towards the outside of the V. In the M5 motor, these are switched so as to minimize the distance from exhaust ports to turbos that can therefore be nestled on the inside of the V. These exceptionally short paths are shown clearly in the above illustration.
Another cause of turbo lag is the inertia of the turbine and compressor. To minimize this, two smaller turbos are used instead of one larger one, and the spinning materials are all exceptionally lightweight.
The turbo on the M5 is shown in more detail below.
The turbo on the M5 is shown in more detail below.
The exhaust turbine (1) takes in gasses from the bottom, turns them 90 degrees (thus spinning the turbine) and shunts them to the exhaust system through the large diameter passages on the left. The compressor (3) is turned via the sealed bearing seat (2). Charge air is taken in from the centre and directed out on top. The vacuum operated wastegate valve (5) and actuator (4) is used to divert exhaust gasses so that they do not hit the turbine in order to control speed and boost.
The following illustration shows the intake airflow.
Air is taken in from the front of the car through the intake snorkel (1) into the intake silencers and air filters (2) past an air mass sensor (3). Cleaned air from the crankcase ventilation system is connected at (4). The turbo then pressurizes the air and sends it to a charge air cooler (6 - discussed in more detail below) and past a charge air pressure sensor (7). The air passes through a throttle valve (8) into the intake manifold (9) and from there into the cylinders. A charge air pressure and temperature sensor is located at (10). A connection from the tank vent valve is made at (11) for dirty gasses to be recycled back into the intake.
Most turbos have a blow-off valve which is used to dump pressure from the charge air system when the accelerator is suddenly released. Normally, this causes the compressed air to suddenly have no place to go, and the surge in pressure can damage the system (called "pump"). However, the combination of the design of the compressor vanes, Valvetronic and computer control make the system insensitive to pump, and hence no blow-off valve is needed.
To help further reduce turbo lag, when in "Sport" engine mode the wastegate is kept closed longer. This leads to increased fuel consumption as the exhaust is backed up, but increases response as the turbos are kept better spooled up in case they are needed.
One consequence of the compression of the air is that it heats up to over 130 C. To allow more fuel to be mixed in and keep the compression ratio in the cylinders up, the charge air is cooled by two very large water-cooled charge air coolers back to around 50 C. These are especially large to promote better cooling, to de-throttle the intake air, and to reduce the distance to promote faster throttle response. The charge air coolers are the two prominent metal boxes at the front of the engine.
The charge air coolers are water cooled from a low temperature cooling circuit separate from the engine cooling circuit. The same liquid cooling circuit is shared with the DME (Digital Motor Electronics) computers which are sitting on the diagonal at the back near the firewall, one per cylinder bank, with the master DME on driver's right.
The turbos themselves can get very hot with the >1000 C exhaust temperatures, and are also water-cooled from the main engine cooling circuit (the metal pipes sitting on top of the intake system are for coolant). A particular issue with turbos is "heat soak" after the car is turned off. The exhaust manifold is still very hot, and the heat soaks into the turbine bearings, damaging them over time. To prevent this, the cooling circuit and main fan is kept going even after the engine is turned off until the temperature of the coolant reaches a reasonable value.
Due to the standard V8 crankshaft considerations, the design of the crankshaft is a crossplane design (see my blog post V8 Crankshaft). However, this inevitably leads to a less than ideal cylinder firing order, which is responsible for the "burble" you hear in a typical V8.
The problem with the V8 burble is that the exhaust pulses on each cylinder bank are irregular. This tends to throttle the exhaust flow. In the case of a turbocharger, the irregular pulses lead to a pulsating acceleration and deceleration of the exhaust turbines which is inefficient. To counteract this problem, BMW designed an ingenious (and patented) "crossbank exhaust manifold".
The illustration above gives the official BMW cylinder numbering convention for V8s, and gives the cylinder firing order in brackets. Note how cylinders 8 and 6 (on the same bank) fire one after another, as do cylinders 2 and 1 The crossplane crankshaft forces this firing order (including the two adjacent cylinders 1 and 2 firing one right after the other which causes heat buildup issues on the cylinder wall they share).
However, despite the uneven firing order, the design of the crossbank exhaust manifold ensures that the turbos each get alternate exhaust pulses, and within each turbo, the pulses alternate between the two scrolls.
An overview of the entire system air intake and exhaust is diagrammed below. The front of the car is on top.
The air flows into the intake silencers (4), pass the air mass sensors (5) and into the turbos (6). The air is compressed and sent to the charge air coolers (3) where they pass a temperature and pressure sensor (2), through a throttle (1) and into the intake manifold where the pressure is again monitored (13). From there, the intake valves lift and draw the air into the cylinders on the intake stroke, mix fuel in on the compression stroke and then combust, driving the pistons down for the power stroke.
On the exhaust stroke the exhaust valves open and the returning piston drives the hot exhaust gasses out into the exhaust manifold where they are crossed over and enter into the turbos (6). A wastegate valve (7) operated by an electro-pneumatic pressure converter (8) is used to slow down the turbines when necessary. The exhaust gasses then flow out to the exhaust through the catalytic converters (11), which includes a control oxygen sensor (9) and a monitoring oxygen sensor (10).
All of this is controlled by two Digital Motor Electronics (DME) computers (12), one controlling each cylinder bank with the one on the right of the diagram being the master.
The wastegate valves on the turbos are operated by vacuum pressure. Electronically controlled electromagnets (solenoids) open and close under computer control. This allows vacuum pressure or atmospheric pressure onto one side of the wastegate control, which moves the wastegate valve open and closed. Because of the turbo-charged nature of the engine, vacuum is sometimes in short supply as compared to a naturally aspirated car which operates with the intake manifold in a constant state of vacuum.
Therefore there is an electric pump (1) that generates the vacuum, and it does not at all rely upon the intake manifold vacuum (or lack of it).
The vacuum system generates and stores energy in a vacuum reservoir (6) to power the power brakes (via connection 2) and the wastegate valves (4) on the turbos (via the electro-pneumatic switch 5).
BMW took quite some to move to turbocharged engines, but the move eventually became inevitable as the only way of increasing output while adding low end torque and controlling emissions and fuel economy. However, BMW was keen to ensure that the driving experience remained consistent with an NA engine, and so went to great lengths, especially in the M5, to eliminate turbo lag.
The wastegate valves on the turbos are operated by vacuum pressure. Electronically controlled electromagnets (solenoids) open and close under computer control. This allows vacuum pressure or atmospheric pressure onto one side of the wastegate control, which moves the wastegate valve open and closed. Because of the turbo-charged nature of the engine, vacuum is sometimes in short supply as compared to a naturally aspirated car which operates with the intake manifold in a constant state of vacuum.
Therefore there is an electric pump (1) that generates the vacuum, and it does not at all rely upon the intake manifold vacuum (or lack of it).
The vacuum system generates and stores energy in a vacuum reservoir (6) to power the power brakes (via connection 2) and the wastegate valves (4) on the turbos (via the electro-pneumatic switch 5).
BMW took quite some to move to turbocharged engines, but the move eventually became inevitable as the only way of increasing output while adding low end torque and controlling emissions and fuel economy. However, BMW was keen to ensure that the driving experience remained consistent with an NA engine, and so went to great lengths, especially in the M5, to eliminate turbo lag.